
量子化学Ⅰレポート
応用化学科 g940851
小林 篤
課題.炭素原子6個からなる炭化水素の全ての異性体を
Huckel法で計算し、構造と安定性について考察せよ。1)

永年方程式は
-λ 1 0 0 0 0 ①ε=α+1.1820β1 –
λ 1 0 0 0 ②ε=α+1.2470β0 1 –
λ 1 0 0 =0 ③ε=α+0.4450β0 0 1 –
λ 1 0 ④ε=α-0.4450β0 0 0 1 –
λ 1 ⑤ε=α-1.2470β0 0 0 0 1 –
λ ⑥ε=α-1.1820β6
個のπ電子がエネルギーの低い軌道から順番に2つずつ入るので、βが負であることを考慮して,①~③までに全て入り、安定である。2)
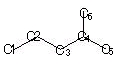
永年方程式は
-λ 1 0 0 0 0 ①ε=α+1.9021β1 –
λ 1 0 0 0 ②ε=α+1.1756β0 1 –
λ 1 0 0 =0 ③ε=α0 0 1 –
λ 1 1 ④ε=α0 0 0 1 –
λ 0 ⑤ε=α-1.1756β0 0 0 1 0 –
λ ⑥ε=α-1.9021β3)
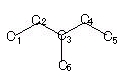
永年方程式は
-λ 1 0 0 0 0 ①ε=α+1.9319β1 –
λ 1 0 0 0 ②ε=α+β0 1 –
λ 1 0 1 =0 ③ε=α+0.5176β0 0 1 –
λ 1 0 ④ε=α-0.5176β0 0 0 1 –
λ 0 ⑤ε=α-β0 0 1 0 0 –
λ ⑥ε=α-1.9319β4)
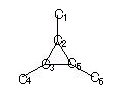
永年方程式は
-λ 1 0 0 0 0 ①ε=α+2.4142β1 –
λ 1 0 1 0 ②ε=α+0.6180β0 1 –
λ 1 1 0 =0 ③ε=α+0.6180β0 0 1 –
λ 0 0 ④ε=α-0.4142β0 1 0 1 –
λ 1 ⑤ε=α-1.6180β0 0 0 0 1 –
λ ⑥ε=α-1.6180β5)

永年方程式は
-λ 1 1 0 0 0 ①ε=α+2.2283β1 –
λ 1 0 0 0 ②ε=α+1.3604β1 1 –
λ 1 0 0 =0 ③ε=α+0.1859β0 0 1 –
λ 1 0 ④ε=α-β0 0 0 1 –
λ 1 ⑤ε=α-β0 0 0 0 1 –
λ ⑥ε=α-1.7746β6)

永年方程式は
-λ 1 0 0 0 1 ①ε=α+2β1 –
λ 1 0 0 0 ②ε=α+β0 1 –
λ 1 0 0 =0 ③ε=α+β0 0 1 –
λ 1 0 ④ε=α-β0 0 0 1 –
λ 1 ⑤ε=α-β1 0 0 0 1 –
λ ⑥ε=α-2β以上の6つの例を挙げてみたが、1)で述べたようにπ電子は全てエネルギー準位の低い軌道から入っていく。そこで
1つの目安として、電子の入っている軌道のエネルギーを全て合計してみると、1)が最大で番号順に下がり、6)で最小となる。大体だが、対称性があったり、環状であれば安定な物質であるということが分かる。